Magnetic forces (forces of attraction, forces of repulsion)
What are magnetic forces?
Magnetic forces can be felt when a magnet is brought close to a ferromagnetic material or another magnet. The cause of magnetic forces are electric currents, i.e. the movement of charges. In electromagnetism, on the other hand, there are also electric forces that emanate from charges at rest and act on other charges. In permanent magnets, minute circular currents are responsible for the magnetic forces. Electromagnets, by contrast, are operated directly by a current flowing through a coil.Table of Contents
Magnetic forces are a noticeable effect of force that can generally be detected between moving charges, i.e.
between currents.
Magnetic substances exert forces on each other or on ferromagnetic
materials.
In magnets, the effect of force is also attributed to minute circular currents in the material.
Three fundamental forces
In physics, there are only 3 different fundamental forces that are the cause of all known effects of force. These are gravity, electromagnetism and nuclear forces. The nuclear forces can be subdivided even further, but they usually play no role in the forces that humans can observe in their environment.Gravity
Gravity, on the other hand, always plays a role when a lot of mass is involved. Even with very large masses, however, the effect of gravity can only be detected with great technical effort. Strong gravitational forces only emanate from interstellar objects such as moons, planets and stars. The mass of the earth, for example, exerts sufficient gravity on all objects to bind them to its surface with a noticeable force. Tidal forces and the movement of planets and stars are, therefore, primarily determined by gravity. Gravitational forces are greater than any other force in large stars with enormous masses, so gravity can overcome any kind of resistance. As a result, gravitational forces can cause stars to collapse into black holes. In everyday life, however, we only observe gravitational force as the earth’s gravity between objects and the earth itself. Gravity between objects in our environment, on the other hand, is so small that we hardly notice it.Electromagnetic force
All other forces that we observe in everyday life are electromagnetic in nature. Electromagnetic forces can be divided into electric forces and magnetic forces.Electric forces
When a substance carries a charge, electric forces are at work. If unequally charged objects (i.e. a positively charged object and a negatively charged object) touch each other, charge equalisation occurs. Afterwards, no electric force can be perceived anymore. Equally charged objects (i.e. both negatively or both positively charged) always repel each other, and unequally charged objects (one negative, one positive) always attract each other.Effects of magnetic force are not caused directly by the charges.
Magnetic charges do not exist.
Magnetic forces
Magnetic forces are caused by elementary magnets in the material, which are created by minute circular currents with a measurable magnetic moment. The electron spin is usually the strongest elementary magnet in the material. A magnetic effect of force occurs when neighbouring electron spins are aligned in parallel.The forces of a magnet can be destroyed if the alignment of the elementary magnets in the material is jumbled. This can be caused by heating or heavy blows to the magnet. A strong magnet can also demagnetise a weaker magnet or reverse its polarisation.
In addition, there is the force a magnetic field exerts on a moving charge, which is known as the Lorentz force. When a charge moves in a magnetic field, a force acts perpendicular to the magnetic field and the direction of movement of the charge if the movement and magnetic field themselves are not completely parallel to one another. This is the Lorentz force.
There is a reason why electric and magnetic forces are combined into electromagnetism.
Moving charges always generate magnetic forces. Magnetic fields exist exclusively due to charge movement, which always creates a magnetic field with a north pole and a south pole. There are no intrinsic sources of the magnetic field, such as the charge is the source of the electric field. In electromagnets, for example, a strong current flows through a coil, creating a strong effect of magnetic force.
Likewise, the magnetic forces of permanent magnets are also caused by microscopic charge movement in matter. Charges at rest, on the other hand, emanate electric forces. So, charges cause magnetic forces when in motion and electric forces when at rest. Magnetic and electric forces must, therefore, transmute into each other through a transformation of the state of motion. This is described mathematically by electrodynamics, the theory of electromagnetism.
Magnetic forces always act along the magnetic field. This can be represented by field lines. The field lines subsequently also indicate the direction of the magnetic forces, and the magnitude of the effect of force increases with the density of the magnetic field lines.
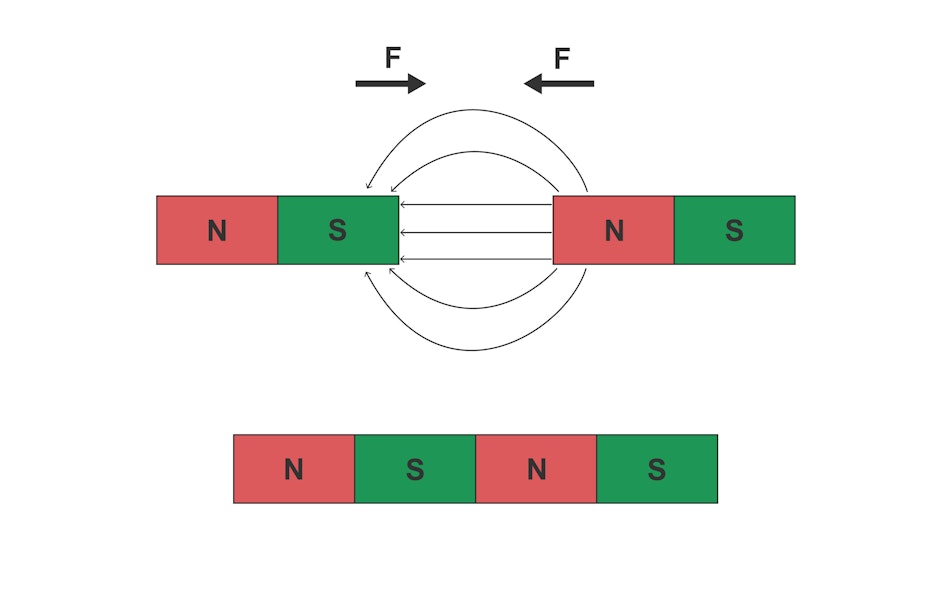
Shown above are two permanent magnets facing each other with two different poles.
The field lines then run from the north pole of one magnet to the south pole of the other magnet (and further inside the material).
A force F acts along these field lines, attempting to bring the two magnets closer together.
The magnetic field lines symbolise a magnetic flux and, therefore, magnetic energy between the two permanent magnets.
If the two magnets touch each other, the energy of this field between the two magnets is minimised.
In physics, forces always act in the direction of an energetic minimum.
It is also possible to conceive the magnetic forces as a physical principle for minimising the total energy of a system.
For example, an object falls to the ground due to the force of gravity because it has minimal potential energy on the ground.
Even two magnets facing each other, as well as a magnet located at a certain distance from a ferromagnetic plate, can still minimise the total energy of the "overall system".
There is magnetic energy between the magnets or between a magnet and an iron plate. The magnitude of the field energy of a magnet is described by the energy product.
When the magnets approach each other, the magnetic energy of the air space is reduced. If the magnets touch each other, the air space and therefore the field energy in this area is zero and thereby minimal. Physically, forces always act in the direction of an energetic minimum. The magnitude of the force is proportional to the change in magnetic energy when the magnets approach each other.
As a general rule, the following applies to every force \( \vec{F}\) in an energy potential U:
\( \vec{F}=-\vec{\nabla}U\)
\( \vec{\nabla}\) denotes the "derivative vector" in all spatial directions (mathematically also called "gradient") and can be written as
\( \vec{\nabla}=\left(\begin{array}{ccccc} \frac{\partial}{\partial{x}} & & \frac{\partial}{\partial{y}} & & \frac{\partial}{\partial{z}} \end{array}\right) \)
where \(\frac{\partial}{\partial{x}}\) denotes the "change" along the x-axis, i.e. the partial differentiation according to x.
If the change in energy is particularly strong in one direction in the potential U,
then a particularly strong force is acting in that direction.
The magnitude of magnetic and electric fields subject to currents and charges is mathematically described in precise detail by Maxwell's equations.
Maxwell's equations are very complex to solve.
However, there are approximation formulae, some better than others, such as for calculating the magnetic force on the surface of a cylindrical electromagnet, for example.
For that, the magnetic field H can first be calculated using an approximation:
\(H=\frac{nI}{\sqrt{l^2+4R^2}}\)
where n is the number of turns of the coil of the electromagnet, l is the length of the coil, R is the radius of the coil and I is the current through the coil.
For a cylindrical magnet with magnetic flux density B
and a pole face A,
the force F
can be calculated by aproximation as follows:
\(F=\frac{1}{\mu\mu_0}AB^2\)
where μ0 denotes the magnetic permeability of the vacuum and μ the magnetic permeability of the material exposed to the B field.
Since the magnetic flux density B can easily be calculated from the magnetic field H:
\(H=\frac{1}{\mu\mu_0}B\)
the magnetic force can also be calculated for the coil and, applying the formula for the pole face A as a function of the magnetic radius R, namely \(A={\pi}R^2\), it follows that:
\(F=\frac{1}{\mu\mu_0}AB^2=\mu\mu_0AH^2=\mu\mu_0H^2{\pi}R^2\)
For the special case of the cylindrical coil with radius R and length l, it is:
\(F=\mu\mu_0H^2{\pi}R^2=\frac{\mu\mu_0{\pi}R^2n^2I^2}{(l^2+4R^2)}\)
For an electromagnet with a radius R=3 cm at a current I of 10 amperes in a coil with n=1 000 turns and a coil length of l=10 cm hence approximately:
\(F=\frac{\mu\mu_0{\pi}R^2n^2I^2}{(l^2+4R^2)}=\frac{4{\pi}\cdot10^{-7}\cdot9\cdot10^{-4}\cdot{\pi}\cdot10^6\cdot10^2}{10^{-2}+4\cdot9\cdot10^{-4}}\) = 26,1 N
The electromagnet could therefore lift approximately 26,1 newtons, which corresponds to around 2,7 kg. This is not a lot for a current of 10 amperes. Consequently, iron cores are often used in electromagnets because they increase the effect of magnetic force many times over, thanks to the significantly higher magnetic permeability μ of the iron.
Illustrative material
All our magnet applications are based on these fascinating magnetic forces. The experimental applications are particularly educational:
Author:
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
The copyright for all content in this compendium (text, photos, illustrations, etc.) remains with the author, Franz-Josef Schmitt. The exclusive rights of use for this work remain with Webcraft GmbH, Switzerland (as the operator of supermagnete.nl). Without the explicit permission of Webcraft GmbH, the contents of this compendium may neither be copied nor used for any other purpose. Suggestions to improve or praise for the quality of the work should be sent via e-mail to
[email protected]
© 2008-2024 Webcraft GmbH
© 2008-2024 Webcraft GmbH